FML阅读笔记-1
Published:
我希望自己也是一颗星星。如果我会发光,就不必害怕黑暗。如果我自己是那么美好,那么一切恐惧就可以烟消云散。于是我开始存下了一点希望————如果我能做到,那么我就战胜了寂寞的命运。
FML阅读笔记
接下来,我们将简要介绍一些常见的机器学习场景。这些场景在学习者可用的训练数据类型、接收训练数据的顺序和方法以及用于评估学习算法的测试数据方面有所不同。
- 监督式学习:学习者接收一组标记的示例作为训练数据,并对所有看不见的点进行预测。这是与分类、回归和排名问题相关的最常见方案。上一节中讨论的垃圾邮件检测问题是监督式学习的一个实例。
- 无监督学习:学习者仅接收未标记的训练数据,并对所有看不见的点进行预测。由于该设置中通常没有可用的标记示例,因此很难定量评估学习者的表现。聚类和降维是无监督学习问题的示例。
- 半监督学习:学习者会收到一个由标记和未标记数据组成的训练样本,并对所有看不见的点进行预测。半监督学习在未标记数据易于访问但获得标签成本高昂的环境中很常见。应用程序中出现的各种类型的问题,包括分类、回归或排名任务,都可以被框定为半监督学习的实例。希望学习者可访问的未标记数据的分布可以帮助他取得比在监督环境中更好的表现。分析实现这一目标的条件是许多现代理论和应用机器学习研究的主题。
- 转导推理:与半监督场景一样,学习者会收到一个标记的训练样本以及一组未标记的测试点。然而,转导推理的目标是仅预测这些特定测试点的标签。转导推理似乎是一项更容易的任务,并且与各种现代应用程序中遇到的场景相匹配。然而,与半监督设置一样,在这种设置中可以取得更好表现的假设是尚未完全解决的研究问题。
- 在线学习:与前面的场景相比,在线场景涉及多轮训练和测试阶段混合在一起。在每一轮中,学习器都会收到一个未标记的训练点,进行预测,收到真实标签,并产生损失。在线设置的目标是最小化所有轮次的累积损失或最小化遗憾,即发生的累积损失与事后最佳专家的累积损失之间的差异。与前面讨论的设置不同,在线学习中没有进行分布假设。事实上,在这种情况下,实例及其标签可能是以对抗方式选择的。
- 强化学习:训练和测试阶段也在强化学习中混合在一起。为了收集信息,学习者会主动与环境交互,在某些情况下会影响环境,并且每次操作都会立即获得奖励。学习器的目标是在一系列操作和迭代环境中最大化他的奖励。但是,环境不提供长期奖励反馈,学习者面临着探索与利用的困境,因为他必须在探索未知操作以获取更多信息与利用已收集的信息之间做出选择。
- 主动学习:学习者以自适应或交互方式收集训练示例,通常是通过查询 oracle 来请求新点的标签。主动学习的目标是实现与标准监督学习场景(或被动学习场景)相当的性能,但标记的示例更少。主动学习通常用于获得标签成本高昂的应用,例如计算生物学应用。
泛化
机器学习从根本上讲是关于泛化的。例如,标准的监督学习场景包括使用标记样本的有限样本来准确预测看不见的样本。该问题通常表述为从假设集中选择一个函数,该假设集是所有函数系列的子集。所选函数随后用于标记所有实例,包括未见过的示例。应该如何选择假设集?设置丰富或复杂的假设后,学习者可以选择与训练样本一致的函数或预测器,即对训练样本不犯错误的函数或预测器。对于不太复杂的系列,在训练样本上产生一些错误可能是不可避免的。这将导致更好的泛化?我们应该如何定义假设集的复杂性?
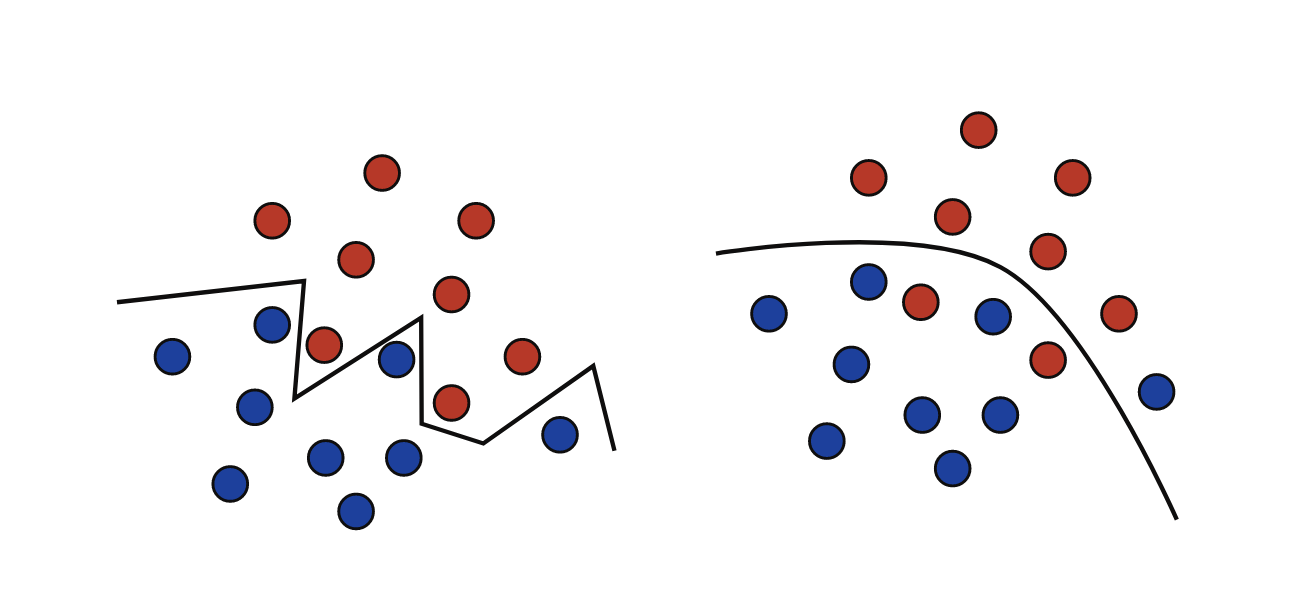
下图说明了这两种类型的解决方案:一种是一条锯齿形线,它完美地分隔了蓝色和红色点的两个群体,并且是从复杂的族中选择的;另一个是从更简单的系列中选择的一条更平滑的线,该线只是不完美地区分了这两组。我们将看到,一般来说,训练样本上的最佳预测因子可能不是总体上最好的。从非常复杂的系列中选择的预测因子基本上可以记住数据,但泛化与训练标签的记忆不同。我们将看到样本量和复杂性之间的权衡在泛化中起着关键作用。当样本量相对较小时,从过于复杂的族中进行选择可能会导致泛化效果不佳,这也称为过拟合。另一方面,对于太简单的族,可能无法获得足够的精度,这称为欠拟合。
我们希望用 PAC 理论在解释以下几个问题:
- 什么样的问题能够被有效率的学习 (What can be learned efficiently)?
- 什么样的问题天生无法有效地被学习 (What is inherently hard to learn)?
- 成功的学习需要多少样本 (How many examples are needed to learn successfully)?
- 学习有没有一个综合性的模型指导 (Is there a general model of learning)?
1. PAC学习的动机与背景
PAC理论的核心思想是,机器学习中的学习过程并非总能提供完美的预测模型,因为训练数据有限、噪声不可避免、以及数据分布的复杂性。这时候,我们的目标就变成了寻找一种”近似正确”的模型——它不一定在所有数据上都表现完美,但在大多数情况下表现良好。此外,这个模型是”概率”上近似正确的,意味着它在绝大部分随机样本上有较高概率表现得近似正确。
Why PAC? 之所以称为”概率近似正确”,是因为它结合了概率和近似两方面:
• 概率(probably):表示模型在大多数情况下能够提供合理的预测,虽然不是总是完美。
• 近似正确(approximately correct):模型不必精确匹配目标概念,只需与目标概念足够接近,从而在实践中表现出足够低的误差。
概念定义
PAC理论的学习过程以以下几个基本概念为基础:
在PAC学习中,一个概念 c 是从样本空间 X 到标记空间 Y 的映射,即 $c: X \to Y$ 。对于任何输入样例 $x \in X$ ,概念 c 决定了它的真实标记 $y \in Y$ 。通常,标记空间 Y 是一个离散集合,例如 {0, 1} (用于二分类任务),但它也可以是更广泛的集合,取决于具体的学习任务。
举例来说,假设我们正在进行一个二分类任务,样本空间 X 可以是所有可能的特征向量,而标记空间 Y 是二元集合 {0, 1} 。一个概念 c 就是从 X 中的特征向量映射到二元标签的函数,反映每个样例属于哪个类别。
概念类 (Concept Class)
所有可能的目标概念的集合称为概念类(concept class),用符号 $\mathcal{C}$ 表示。概念类 $\mathcal{C}$ 包含所有我们可能感兴趣的目标概念。例如,假设我们在一个二维平面上进行线性分类,概念类 $\mathcal{C}$ 可以表示所有可能的线性分类器,即每个概念对应一个不同的线性决策边界。
形式化地,概念类 $\mathcal{C}$ 是概念的集合:
\[\mathcal{C}= \{c_1, c_2, \dots, c_n\}\]其中每个 $c_i$ 都是从样本空间 X 到标记空间 Y 的函数。
假设空间 (Hypothesis Space)
- 给定学习算法 $\mathcal{L}$ , 它所考虑的所有可能概念的集合称为假设空间 (Hypothesis Space), 用符号 $\mathcal{H}$ 表示.
若目标概念 $c∈ \mathcal{H}$ , 则 $\mathcal{H}$ 中存在假设能将所有示例按与真实标记一致的方式完全分开,我们称该问题对学习算法是可分的 (Separable), 也可以叫做一致的 (Consistent). 或者按照我们课程上所说是Realizable的.
若目标概念 $c\notin \mathcal{H}$ 或 $c∈ \mathcal{H}$ ,则 $\mathcal{H}$ 中可能存在假设能将所有示例按与真实标记一致的方式完全分开,我们则称该学习算法是 Agnostic 的.
若目标概念 $c\notin \mathcal{H}$ , 则 $\mathcal{H}$ 中不存在假设能将所有示例按与真实标记一致的方式完全分开,我们则称该学习算法是不一致的 (Inconsistent) 的.
定义1. 泛化误差(Generalization Error)
泛化误差(Generalization Error)是指学习算法在新数据(即训练集之外的数据)上的表现。它衡量的是模型对未见过的数据做出正确预测的能力。数学上,泛化误差是指模型预测输出与真实标签之间的差异在整个数据分布 $\mathcal{D}$ 上的期望
给定一个假设 $h \in \mathcal{H}$ ,目标概念 $c \in \mathcal{C}$ ,以及一个底层数据分布 $\mathcal{D}$ ,假设 h 的泛化误差或风险定义为:
\[R(h) = \mathbb{P}{x \sim D}[h(x) \neq c(x)] = \mathbb{E}{x \sim D}[1_{h(x) \neq c(x)}]\]其中 $1_{\omega}$ 是事件 $\omega$ 的指示函数。当假设 $h(x)$ 与目标概念 $c(x)$ 不一致时,指示函数值为 1。泛化误差反映了假设 $h$ 对整个数据分布 $\mathcal{D}$ 的预测错误率。
然而,学习者无法直接访问泛化误差,因为数据分布 $\mathcal{D}$ 和目标概念 c 是未知的。学习者只能通过标记样本 S 来衡量假设的经验误差。
定义2. 经验误差(Empirical error)
给定假设 $h \in \mathcal{H}$ ,目标概念 $c \in \mathcal{C}$ ,以及样本 $S = (x_1, \dots, x_m)$,假设 $h$ 的经验误差或经验风险定义为:
\[\hat{R}_S(h) = \dfrac{1}{m} \sum{i=1}^{m} 1_{h(x_i) \neq c(x_i)},\]其中 m 是样本大小, $1_{h(x_i) \neq c(x_i)}$ 是当假设 $h(x_i)$ 与目标概念 $c(x_i)$ 不一致时的指示函数。经验误差表示假设 $h$ 在样本 $S$ 上的平均错误率。
经验误差是对泛化误差的近似,它衡量了假设在有限样本上的表现,而泛化误差则是基于整个数据分布的期望错误。
由于样本 $S$ 是从分布 $\mathcal{D}$ 独立同分布采样的,且我们想求其在分布 $\mathcal{D}$ 下的期望误差,利用期望的线性性,我们可以将期望运算分开:
\[\mathbb{E}_{S \sim D^m} [\hat{R}S(h)] = \dfrac{1}{m} \sum_{i=1}^{m}\mathbb{E}_{S \sim D^m} \left[ 1_{h(x_i) \neq c(x_i)} \right]=\dfrac{1}{m} \sum_{i=1}^{m}\mathbb{E}_{S \sim D^m} \left[ 1_{h(x) \neq c(x)} \right]\]由于样本 $x_i$ 是从分布 $\mathcal{D}$ 中独立同分布抽样的,因此对于每个 i ,期望是相同的:
\[\mathbb{E}_{S \sim D^m} [1_{h(x_i) \neq c(x_i)}] = \mathbb{E}_{x \sim D} [1_{h(x) \neq c(x)}] = R(h)\]这意味着在 i.i.d. 假设下,经验误差的期望等于泛化误差。换句话说,随着样本量的增加,模型在有限样本上的经验误差将越来越接近其在整个分布上的泛化误差。
定义3. PAC学习(PAC-learning)
给定一个概念类 $\mathcal{C}$ ,我们称其是PAC可学习(PAC-learnable)的,如果存在一个学习算法 A 和一个多项式函数 $\text{poly}(\cdot, \cdot, \cdot, \cdot)$ ,使得对于任意的精度参数 $\epsilon > 0$ 和置信参数 $\delta > 0$ ,对于所有的分布 $\mathcal{D}$ (定义在输入空间 X 上),以及对于任意的目标概念 $c \in C$ ,以下不等式成立:
\[\mathbb{P}_{S \sim D^m }[R(h_S) \leq \epsilon] \geq 1 - \delta\]其中, $m \geq \text{poly}(1/\epsilon, 1/\delta, n, \text{size}(c))$ 。即,存在一个多项式大小的样本量 m ,使得通过算法 A 学习到的假设 $h_S$ 的泛化误差 $R(h_S)$ 不超过 $\epsilon$ (即误差的上限),并且这种情况发生的概率至少是 $1 - \delta$ (即高概率)。如果算法 A 的运行时间也是多项式的,那么我们称 $\mathcal{C}$ 是有效PAC可学习的(efficiently PAC-learnable)。
换句通俗一点的话说就是: 输出假设 h 的泛化误差 $E(h)≤ϵ$ 的概率不小于 $1−δ$.
再换一句更通俗的话说就是: 学习算法能以较大概率 (至少 $1−δ$) 学得目标概念 c 的近似 (误差最大为 ϵ).
沿轴矩形的学习(axis-aligned rectangles)
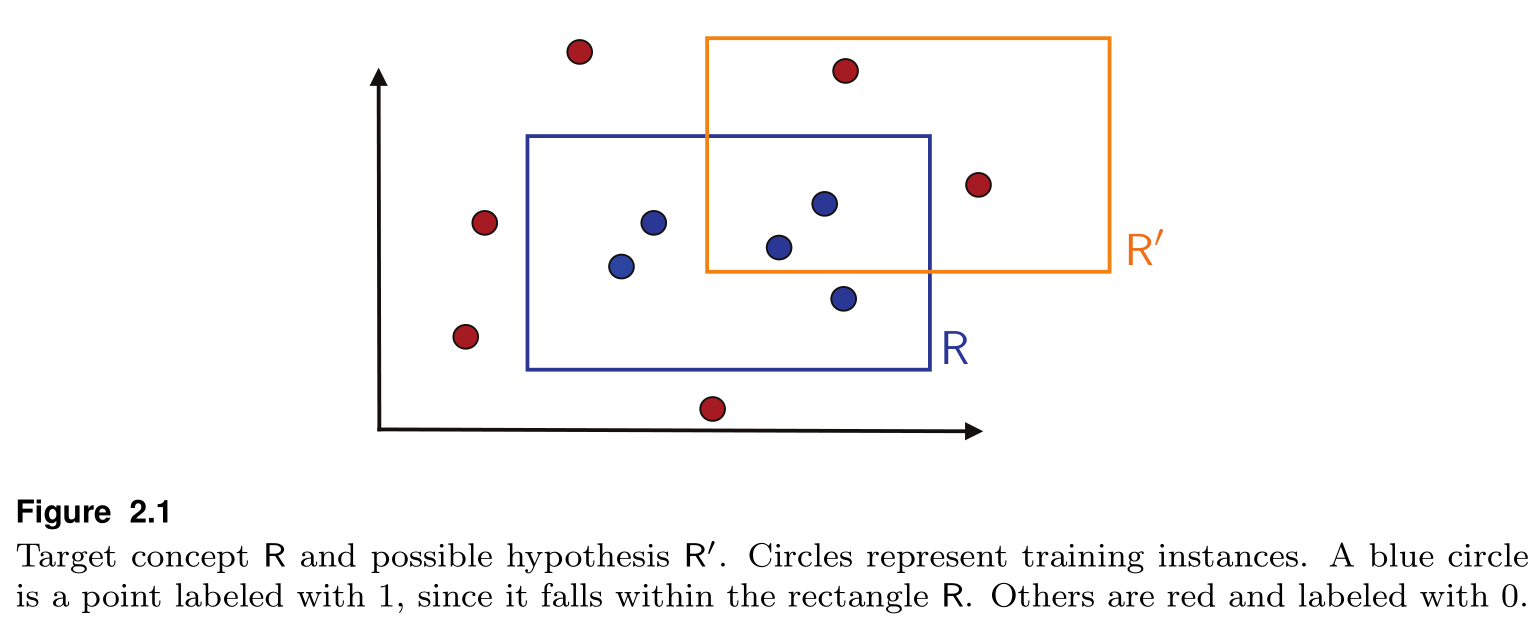
R 是我们要学习的矩形框,矩形框内的样本为正例,框外的样本为负例,R′ 是可能的一个假设.
我们可以证明这种矩形框是PAC可学的——我们设定一个简单的算法:取包裹所有正例样本的最小矩形框,就像这样:
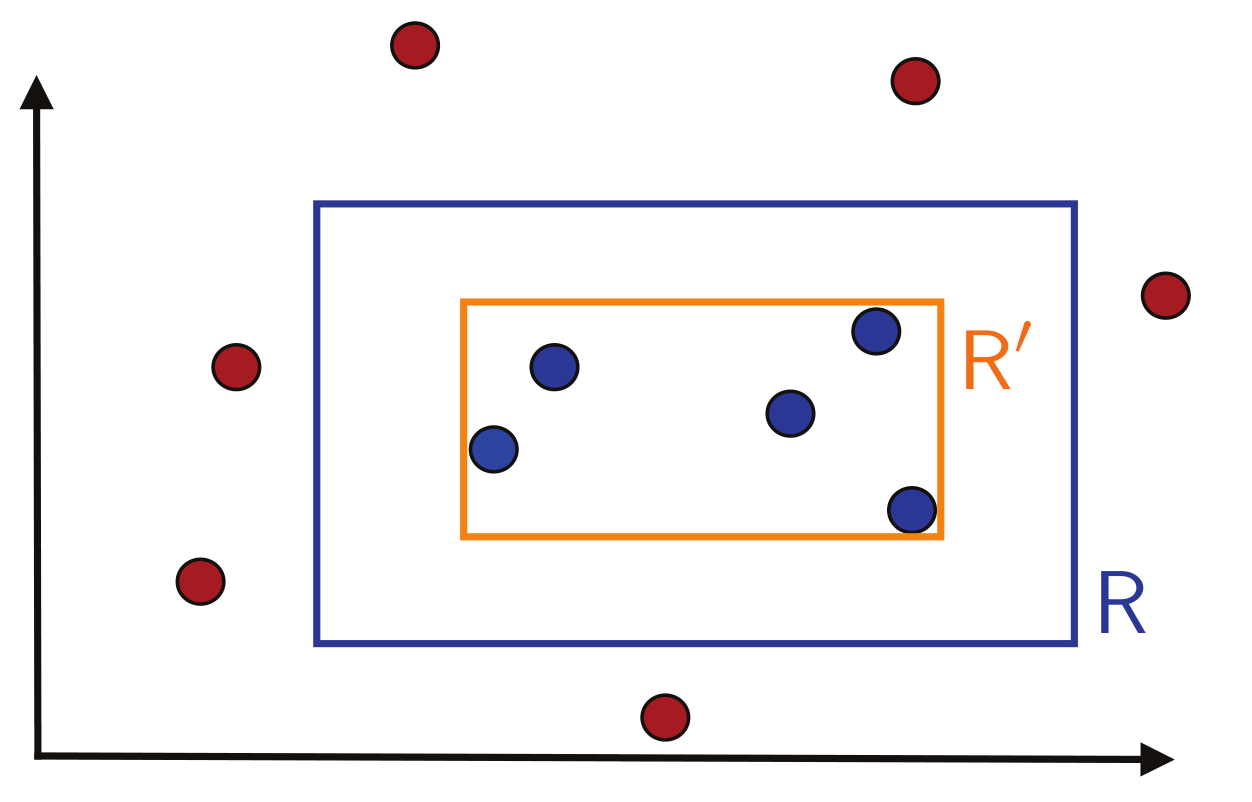
首先,我们先假设样本点由随机分布 $\mathcal{D}$ 产生,用 $\mathbb{P}[R]$ 表示 R 区域的概率质量,即一个样本点落在 R 中的概率.
我们先定义假设框 $R_S$ 的泛化误差 $\mathcal{R}(R_S)$ :样本点落在 $R-R_S$ 区域的期望.
之后我们做一个假设 :
\[\mathbb{P}[R] >\epsilon\]否则, $\mathcal{R}(R_S)<\epsilon$ 显然恒成立
然后我们在举行的四边构建4个小矩形$r_1,r_2,r_3,r_4$, 使得 $\mathbb{P}[r_i] =1/4$
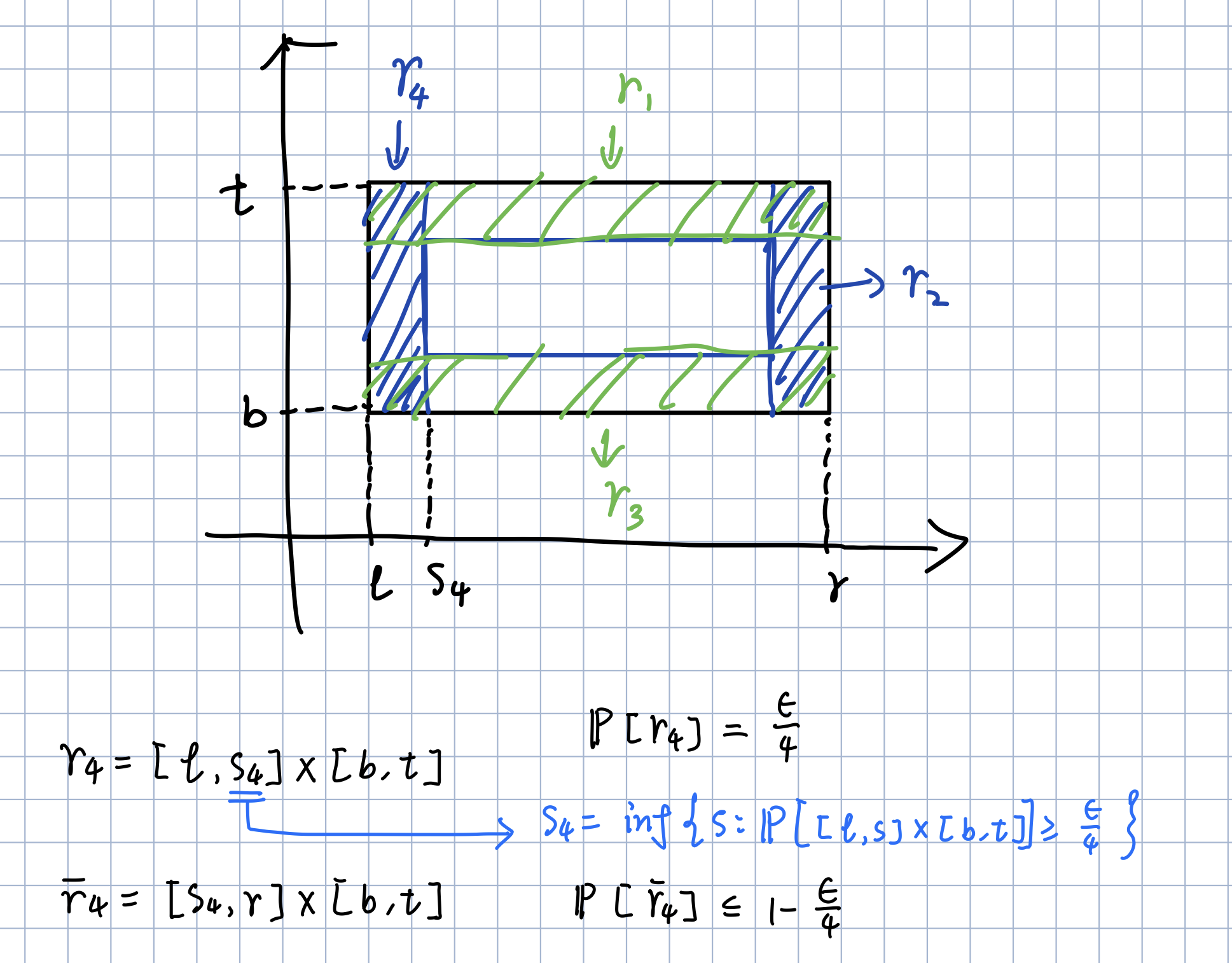
我们记周围这一圈阴影部分为$r=\bigcup^4_{i=1}r_i$,显然有:
\[\mathbb{P}[r] = \mathbb{P} \left[\bigcup_{i=1}^4 r_i \right] \leq\sum_{i=1}^4\mathbb{P}[r_i]\leq\epsilon\]如果我们的假设框 $R_S$ 的四条边都在阴影部分 r 中,即$R−r⊂R_S$,那么有:
\[\mathcal{R}(R_S) = \mathbb{P}[r-R_S] < \mathbb{P}[r]\leq \epsilon\]那么我们考虑其逆否命题:
若 $\mathcal{R}[R_S] > \epsilon$, 可推出 $R - r \nsubseteq R_S$, 也就是说 $R_S$ 至少与 $r_i$ 中的某一个相交为空集, 即 $\bigcup_{i=1}^4 \left( R_S \cap r_i = \emptyset \right)$
A⇒B 说明 $A\subseteq B$ ,即 $P\left[ A \right] \le P\left[ B \right]$
于是上述命题可转化为公式形式:
\[\begin{aligned} \underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right] &\leq \underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \bigcup_{i=1}^4{\left\{ R_S\cap r_i=\emptyset \right\}} \right]\\ &\leq \sum_{i=1}^4{\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \left\{ R_S\cap r_i=\emptyset \right\} \right]}\\ &\leq 4\left( 1-\dfrac{\epsilon}{4} \right) ^m\\ &\leq 4\exp \left( -m\epsilon /4 \right) \end{aligned}\]其中第3行到第4行的转化是重点:我们的假设框 $R_S$ 是由样本 $S$ 生成的,如果假设框与$r_i$不相交,那么必然没有样本点落在 $r_i$ 内对于 m 个样本点都没落进的概率为$\left( 1-\dfrac{\epsilon}{4} \right) ^m$
如果我们要使$\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right] <\delta$ 恒成立,那么需使:
\[4\exp \left( -m\epsilon /4 \right) <\delta\]解得:
\[m>\dfrac{4}{\epsilon}\ln \dfrac{4}{\delta}\]最终得出结论:
当 $m>\dfrac{4}{\epsilon}\ln \dfrac{4}{\delta}$,时,有$\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right] <\delta$ 成立.
泛化界
除此之外,PAC可学性的另一种等价描述可以由泛化界(generalization bound)表示:
在 1−δ 的概率下,泛化误差有关于 m,δ 表示的上界:
\[\mathcal{R}[R_S]\leq \dfrac{4}{m}\ln\dfrac{4}{\delta}\]有限假设集上的学习保证——一致情况
一致(consistent)
有限假说集的学习问题划分为两大类:
- 一致
- 不一致
在有限假设集 H 中,我们要学习的目标概念 c 可以在 H 内,也可以不在 H 内。
如果 $c \in H$ ,我们称这种情况为一致情况(consistent case)。
在一致情况下,我们可以找到一个假设 $h_S \in H$ ,使得它在样本 S 上的经验误差为 0,即 $\hat{R}(h_S) = 0$ 。
例如,在矩形学习的例子中,情况明显是一致的:学到的假设框 $h_S$ 在样本 S 上没有误差。
学习界(Learning bound)
假设我们有一个有限的假设集 H ,其中包含从输入空间 X 到输出空间 Y 的所有可能假设(或函数)。对于一个目标概念 c (即我们想学到的理想函数),若它在 H 中,我们称这种情况为一致情况。
在这种一致的情况下,我们可以找到一个假设 $h_S \in H$ ,使得在训练样本 S 上完全没有误差,即训练误差为 0。这就是说,假设 $h_S$ 在训练样本 S 上表现非常好,完美地分类了所有样本。
核心结论:样本复杂度公式
为了确保模型在训练之外的数据上仍然有较好的表现,我们需要一定数量的样本来训练。给定一个置信水平 $1 - \delta$ (即错误的概率小于 $\delta$ ),如果样本数量 m 满足:
\[m \geq \dfrac{1}{\delta} \left( \log |H| + \log \dfrac{1}{\delta} \right)\]那么我们可以以至少 $1 - \delta$ 的概率确保,假设 $h_S$ 的泛化误差会很小。这意味着,只要样本数量 m 足够大,我们有信心假设 $h_S$ 在新数据上的误差也会很小。
泛化误差上界
上述样本复杂度结果也可以转换成以下泛化误差的公式:
\[R(h_S) \leq \dfrac{1}{m} \left( \log |H| + \log \dfrac{1}{\delta} \right)\]这表示,当我们收集足够多的样本 m 时,以至少 $1 - \delta$ 的概率,假设 $h_S$ 的真实误差 $R(h_S)$ 会小于等于这个上界。
布尔变量的组合
学习布尔变量组合的样本复杂度
假设我们希望学习由多个布尔变量组合而成的目标概念,例如,当目标概念为 $x_1 \land \neg x_2 \land x_4$ 时,示例 (1, 0, 0, 1) 是正样本,而 (1, 0, 0, 0) 是负样本。
概念类的规模
在这种布尔变量组合学习中,每个布尔变量可以有三种状态:正包含、负包含(取反)、或不包含。因此,对于 n 个布尔变量的组合,假设集 H 的大小为 $3^n$ 。
样本复杂度的计算
我们使用样本复杂度公式,以保证学习出的假设在一致的情况下具有较好的泛化能力。对于一个样本复杂度的下界 m ,我们有:
\[m \geq \dfrac{1}{\epsilon} \left( (\log 3)n + \log \dfrac{1}{\delta} \right)\]其中, $\epsilon$ 是允许的泛化误差, $\delta$ 是置信度(例如 $1 - \delta = 98\%$ 表示98%的概率下保证学习效果)。例如,对于 n = 10 、 $\epsilon = 0.1$ 、 $\delta = 0.02$ ,我们得出 $m \geq 149$ ,即需要至少149个样本来确保泛化误差小于0.1,从而达到90%以上的精确度。
一致假设的学习算法
我们基于正样本构建一致假设的一个简单算法:
对于每个正样本 $(b_1, \dots, b_n)$ 和每个布尔变量 i :
• 如果 $b_i = 1$ ,则排除变量 $x_i$ 的否定;
• 如果 $b_i = 0$ ,则排除变量 $x_i$ 。
最终,未被排除的所有变量构成与目标一致的假设。
复杂度分析
对于最多 n 个布尔变量的连词概念类 $C_n$ ,其训练复杂度也是多项式的,每个样本的训练成本为 O(n) 。因此,我们得出该布尔变量组合概念类在 PAC 学习(可学性的一个标准框架)下是可学习的。
有限假设集上的学习保证——不一致情况
学习界
不一致情况下的有限假设集的学习保证
在实践中,假设集 H 中可能没有假设能够与所有训练样本完全一致。这种不一致的情况反映了实际应用中的常见场景,即目标学习问题的复杂性可能超出了算法所使用假设集的表示能力。因此,即使假设 h 在训练样本中存在少量误差,也可能在泛化能力上表现良好。在这种情况下,采用 Hoeffding 不等式可以帮助我们得出有关泛化误差的学习保证。
推论 2.10:Hoeffding 不等式与泛化误差
假设 $h : X \rightarrow {0, 1}$ 为从输入空间到二值输出的假设,对于任何 $\epsilon > 0$ ,以下不等式成立:
\[\mathbb{P}_{S \sim \mathcal{D}^m} \left[ \hat{R}S(h) - R(h) \geq \epsilon \right] \leq \exp(-2m \epsilon^2)\] \[\mathbb{P}_{S \sim \mathcal{D}^m} \left[ \hat{R}S(h) - R(h) \leq -\epsilon \right] \leq \exp(-2m \epsilon^2)\]通过将两者结合,得到以下双侧不等式:
\[\mathbb{P}_{S \sim \mathcal{D}^m} \left[ \mid \hat{R}_S(h) - R(h) \mid \geq \epsilon \right] \leq 2 \exp(-2m \epsilon^2)\]推论 2.11:单个假设的泛化边界
将上述不等式右侧设置为小于等于 $\delta$ ,可以得出单个假设的泛化边界:
\[R(h) \leq \hat{R}_S(h) + \sqrt{\dfrac{\log \dfrac{2}{\delta}}{2m}}\]该不等式表明,对于概率至少 $1 - \delta$ 的情况,我们可以保证假设 h 的真实误差上界。该结果对于有限假设集 H 的学习有以下扩展:
有限假设集的泛化界限
对于有限假设集 H ,可以得出以下界限:
\[R(h) \leq \hat{R}_S(h) + O \left( \sqrt{\dfrac{\log |H|}{m}} \right)\]其中 $\log \mid H \mid $ 表示假设集 H 的编码长度,即所需的位数。该边界显示了样本数量 m 与假设集大小 $\mid H\mid $ 对泛化能力的影响。
• 样本数量增大:可以提高泛化边界,即真实误差的上界更小。
• 假设集大小增大:假设集的复杂性越高,虽然能够更好地拟合训练数据,但泛化边界会因其复杂性而变差。这体现了 奥卡姆剃刀原理:选择较小的假设集可避免过度拟合,并提供更好的泛化性能。
学习场景的普遍性
本节探讨了一些学习场景中的通用方面,为简化说明,之前的讨论中省略了这些内容。
确定性与随机场景
在监督学习的最广泛场景中,数据分布 D 定义在输入空间 X 和标签空间 Y 的联合分布上,即 D 在 $X \times Y$ 上分布。训练样本 S 是从分布 D 中抽样的标记数据,表示为:
\[S = \{(x_1, y_1), \dots, (x_m, y_m)\}\]学习的目标是找到一个假设 $h \in H$ ,使其泛化误差 $R(h) = \mathbb{P}{(x,y) \sim D}[h(x) \neq y] = \mathbb{E}{(x,y) \sim D}[1_{h(x) \neq y}]$ 尽可能小。这种情况称为随机场景,其中输出标签是输入的概率函数。该场景描述了许多实际问题,在这些问题中,输入点的标签并不唯一。比如,当我们根据身高和体重预测性别时,性别标签通常是不唯一的。
为了处理这种场景,可以扩展 PAC 学习框架,引入不可知 PAC 学习的概念:
• 不可知 PAC 学习:假设 H 是假设集。如果存在多项式函数 $\text{poly}(\cdot, \cdot, \cdot, \cdot)$ ,使得对于任意目标概念 $c \in H$ 、误差阈值 $\epsilon > 0$ 和置信度 $\delta > 0$ ,算法 A 能以至少 $1 - \delta$ 的概率输出一个假设 $h_S$ ,满足:
\[R(h_S) - \min_{h \in H} R(h) \leq \epsilon\]即 $h_S$ 的泛化误差接近于假设集中最佳假设的泛化误差。
在随机场景中,当标签可以唯一确定时,称为确定性场景,其中训练数据从 D 中独立抽取,并由唯一的目标函数 f 定义标签。多数学习问题可以在确定性场景下定义,为简单起见,之前的讨论主要集中在该场景中。
贝叶斯误差和噪声
在确定性场景中,目标函数 f 的泛化误差 R(f) 为零。而在随机场景中,即使最佳假设的泛化误差也不为零。
• 贝叶斯误差:给定分布 D ,贝叶斯误差 $R^*$ 是所有可测假设的最小泛化误差:
\[R^* = \inf_{h \text{ 可测}} R(h)\]在随机场景中,贝叶斯误差 $R^*$ 为非零。对于每个 $x \in X$ ,贝叶斯分类器 $h_{\text{Bayes}}$ 是最大化条件概率 $P[y\mid x]$ 的输出 y ,即
\[h_{\text{Bayes}}(x) = \arg\max_{y \in \{0,1\}} P(y|x)\]该分类器的最小误差为 $ \min { P[0 \mid x], P[1 \mid x] } $。
• 噪声:对于每个点 x \in X ,定义噪声为:
\[\text{noise}(x) = \min \{P[1\mid x], P[0\mid x]\}\]平均噪声,即与 D 相关的噪声为 $\mathbb{E}[\text{noise}(x)]$ ,这正是贝叶斯误差 $R^*$ 。噪声反映了学习任务的难度,噪声接近 $\dfrac{1}{2}$ 的样本点较难预测。
